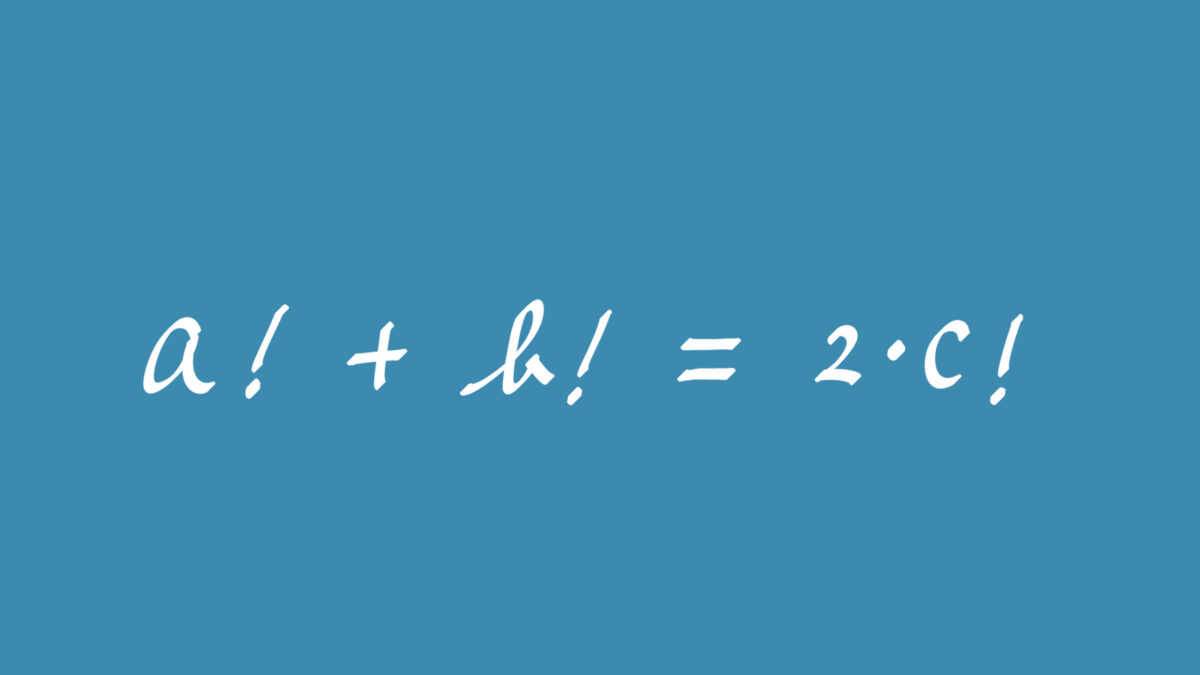こんにちは!今回も九大の問題をいきなり最後から解いていきます。別解として参考にしてください。
今回の別解は、素因数2があるかどうかに注目して解いています。
九州大学2024年・理系前期[3]の(3)解答
方程式 \( a! + b! = 2 \cdot c! \) において,\( a = b = c \) は自明な解である.
上記以外の解があるとする.この時,\( a < b \) として一般性は失わない.
$$ a! + a! < a! + b! < b! + b! $$
より,
$$ 2 \cdot a! < 2 \cdot c! < 2 \cdot b! \, .$$
よって,
$$ a < c < b \, .$$
これより \( b \, – a \ge 2 \) であり,\( b! \) は \( a! \) よりも多くの素因数 \( 2 \) を有する. \( \cdots (\text{i}) \)
ここで,\( a! + b! = 2 \cdot c! \) の両辺を \( a! \) で割って
$$ 1 + \frac{b!}{a!} = 2 \cdot \frac{c!}{a!} \, . \quad \cdots ( \text{ii} ) $$
\( a < c < b \) より, \( b!/a! \) と \( c!/a! \) は整数であり,\( (\text{i}) \) より \( b!/a! \) は偶数である.したがって,\( (\text{ii}) \) の左辺は奇数,右辺は偶数となり矛盾.故に求める解は \( a = b = c \) となるもののみ.//
以上です。階乗 \( n! \) は,具体的な「量」を測るのが難しい(イメージしにくい)対象なので、苦手な人も多いかもしれません。\( n! \) の中にある素因数 \( p \) の個数の求め方など、基本的な知識は押さえておきましょう。
意欲のある現役生は、次の問題も考えてみてください:
「 \( ( a + b )! = a! + b! \) を満たす自然数の組 \( (a, b) \) をすべて求めよ.」
ホームページ上での数式の表示が楽にできるようになったので、これからさらに充実した数学の記事を作成できそうです。今後もよろしくお願いいたします。